How to accurately compute VSYNC timing information from a noisy signal

How to accurately compute VSYNC timing information
from a noisy vsync signal source -- November 24, 2016

Getting a time 'around' the VSYNC time is easy: (1) In native code, obtain vsync times using various native methods (under Windows, DwmGetCompositionTimingInfo() is one possible way). OR, (2) in HTML5, there is a new requestAnimationFrame call, intended to allow animations to smoothly hook into web browser internals, which is already rendering frames for the display:

window.requestAnimationFrame(rafcallback);

All web browsers attempt to synchronize animation callbacks to the actual display VSYNC signal, which allows us (via JavaScript) to discover the "tNow" time of each callback, which is 'usually' very near to VSYNC:

function rafcallback( tFrame ) { var tNow = performance.now(); // this time is 'usually' very near VSYNC ... }

So, the only information we have access to (in a web page) is an approximate/noisy "tNow" values -- and nothing else!

FYI: There is a "tFrame" time argument passed to the rAF callback. Most browsers simply pass in the now() time. However, Chrome passes in the vsync time obtained from the OS. Firefox passes in a completely FAKED time.

But the problem is NOISE!: But the huge problem is that the "tNow" times can be a noisy signal. Each "tNow" may have an ERR of up to several milliseconds (sometimes more!) and there will even be completely missing frames/times. Even the vsync times in native code can sometimes be noisy! In mathematical terms, the "tNow" the rAF callback sees is defined by the following equation, which is just the familiar line formula y=mx+b, but with an additional error term:

tNow = tInterval × nFrame + tTimebase + ERR

The goal: The goal is to create an algorithm that can extract/compute an incredibly accurate "tTimebase" and "tInterval" from the above formula using ONLY the numerous, but noisy, "tNow" times seen. The complication is the impact of the "ERR" term, missing frames, etc.

In Chrome, "ERR" can be up to 1 ms on fast systems, up to 2ms on slower systems, and up to 4ms on notebooks running on battery power.

In Firefox under Windows, the "ERR" term can (1) be all over the place, and (2) permanently phase shifted several milliseconds past true vsync. See Firefox is broken for details.

One solution: One solution (of many) can be found at displayhz.com and in the HTML source at vsynctester.com in the "var HZ=" object. In summary, the algorithm is:

Filter incoming tNow frame times: Discard times where a run of several inter-frame times are not 'stable'. The goal is to filter out all major jitter, leaving only times with minor jitter remaining (Y values). Also filter to account for (slow) browser startup/overhead, and being run in an inactive web browser tab.
Compute a (one-time) first/rough "tInterval" from an initial set of filtered times.
Every so often, compute a 'line of best fit' (needs X values, computed from smoothed times and a 'prior' "tInterval"), which generates a "tTimebase" and a new "tInterval" (for the next iteration).
Adjust the computed "tTimebase" such that all "ERR" terms in the 'line of best fit' are non-negative.
Validate the results. If there is too much variation in the "ERR" terms, start over.
Allow the algorithm to be run over an extended period of time, while still using a fixed memory and cpu overhead.

Algorithm validation: Chrome is the only web browser that (reliably) passes an accurate true vsync time to the rAF callback (as the time argument). vsynctester.com displays this as the 'late' line in the performance graph (in purple). When displayed against the "tTimebase" and "tInterval" line the algorithm computed (in blue), there is a perfect match (the two lines nearly overlap, but with an very tiny and expected phase shift), which validates that the algorithm works:

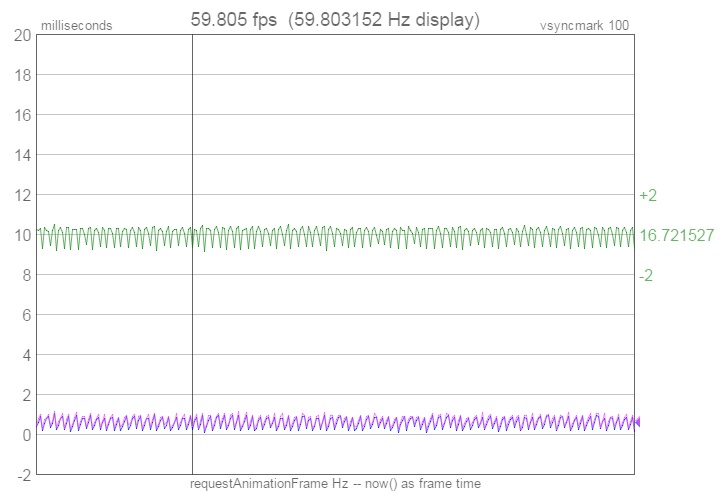
Conclusion: The algorithm in practice works incredibly well. It is able to 'lock into' the VSYNC "tTimebase" and "tInterval" with a high degree of accuracy in very little time (within seconds).

Use rAF time: If running Chrome on Windows, visit vsynctester.com, click on the gear icon, check the "Use rAF time arg as frame time" option, which will then feed the vsync time Chrome obtained from the OS into the algorithm -- and watch how quickly an accurate Hertz value is computed.

Reducing ERR: Regardless of how many frames there are, the ERR term is added at the end -- which means that the ERR is effectively spread over that many frames. So the more frames you sample, the smaller the error per frame becomes, and the more accurately "tInterval" will be computed. And then the best fit line formula finds a (consistent) 'path' through the 'ERR' jitter that further reduces the 'ERR' impact.
Analogy: What is the height of ONE quarter? Measure one quarter and you will be off by 'ERR' (how accurately you can measure anything). But now stack 100 quarters and measure all 100. Your measurement will still be off by 'ERR'. But then you divide your answer by 100 to obtain the height of one quarter, and you have effectively divided your 'ERR' by 100 as well!